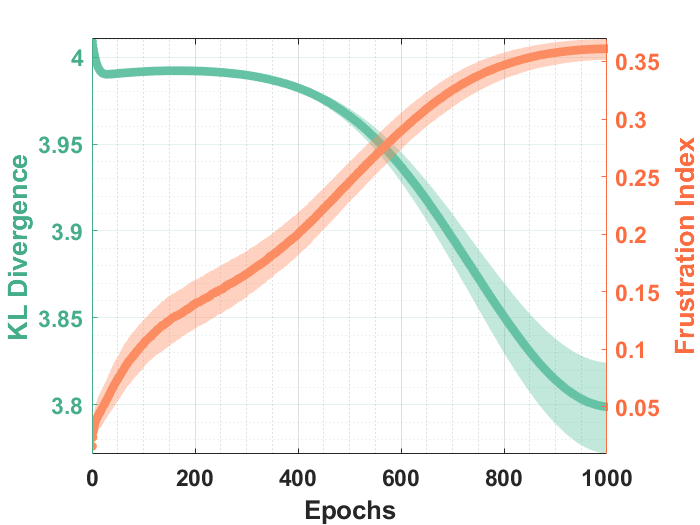
On a signed graph (or spin glass), often times there are interactions that cannot be satisfied regardless of how one assigns the spin states. This property is known as frustration. The study of frustration of a bipartite graph is an active topic in graph theory, and has some important applications in unsupervised learning. For instance, a highly frustrated RBM has several desirable statistical properties, such as the correspondence between the joint and marginal distribution, that can be leveraged to achieve more efficient training.
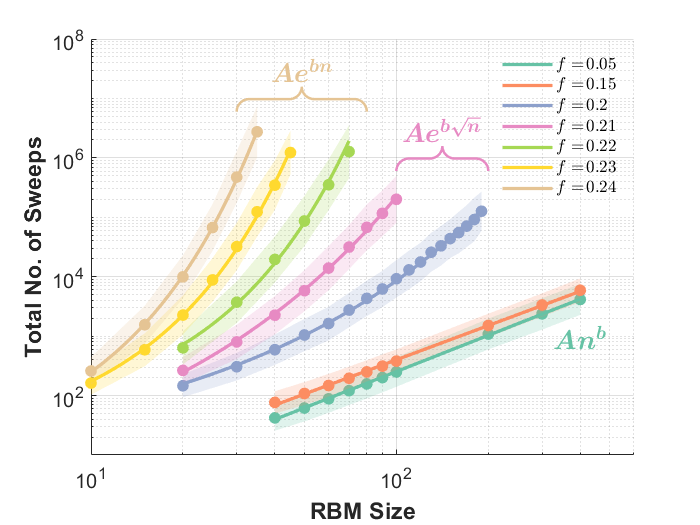
There is some numerical evidence that the complexity of a bipartite glass (or RBM) may display a double phase-transition as the frustration ratio is increased.
The frustration ratio may also be used as a proxy (in place of KL-divergence) in monitoring the training progress of the RBM, as it is expected to be more easily estimated.