I do cool stuff.
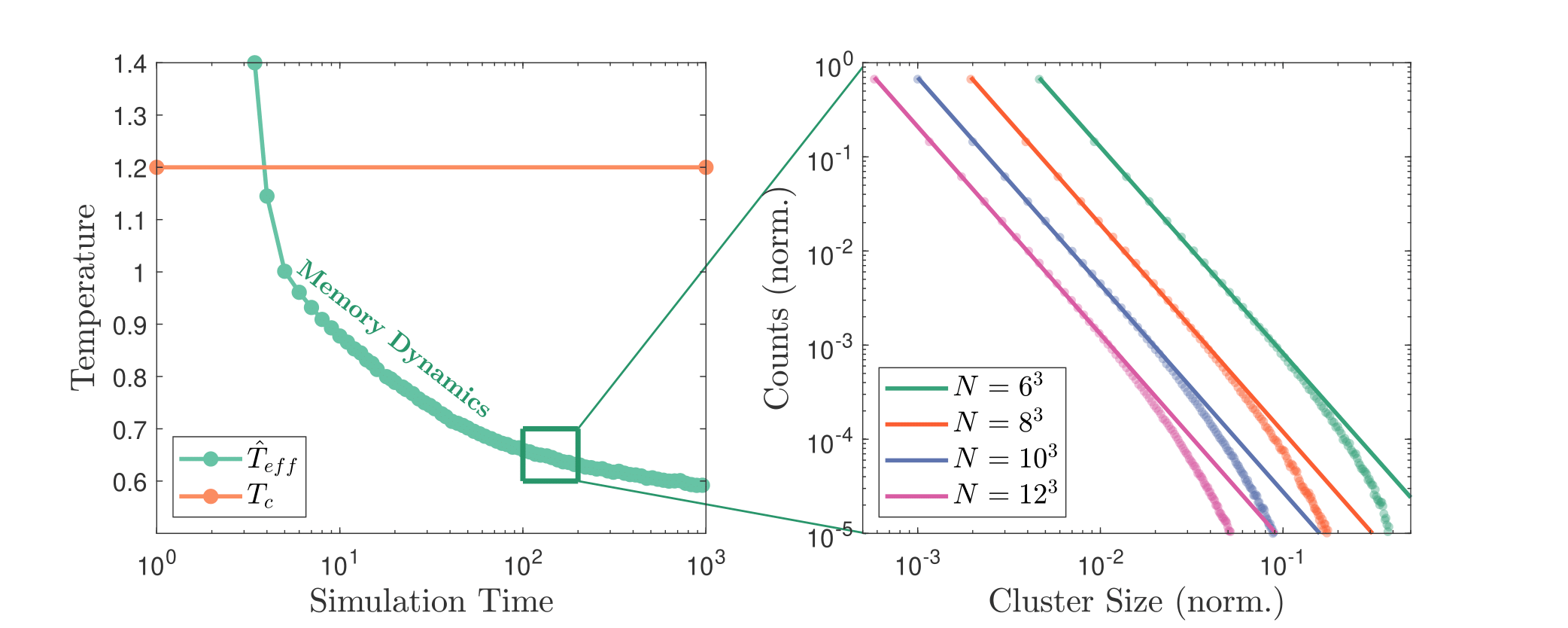
Simulating spin glasses at scale has always been a pain — Python is too slow, and C++ is too painful. Peapods is my attempt at a middle ground: a Monte Carlo package for Ising spin systems where the hot loops are written in Rust and everything else stays in Python, glued together with PyO3. You just pip install peapods and go. ...
Dynamo is NVIDIA’s open-source datacenter-scale distributed inference serving framework for generative AI and reasoning models. Built in Rust for performance and Python for extensibility, it supports disaggregated prefill and decode, dynamic GPU scheduling, and LLM-aware request routing across multi-node multi-GPU topologies. The project has 6k+ GitHub stars and supports backends including TensorRT-LLM, vLLM, and SGLang. ...
While working at BrainChip, I led the research and software-hardware codesign of TENNs (Temporal Neural Networks) — a family of deep state-space models designed for efficient, low-latency inference on edge hardware. This line of work developed in parallel with the broader SSM wave (Mamba, Gated Delta Net, etc.), cross-pollinating ideas around structured recurrences, parallel scans, and kernel parameterizations. ...
Unlike ferromagnetic spin models, a spin glass has a highly non-trivial phase transition profile. For mean field models (the SK spin glass), the glass experiences a replica-symmetry breaking phenomenon that is only fully understood recently. However, for short-range models, almost nothing is known rigorously, including basic problems such as the nature of the glass transition. A potential route towards settling such problems may rely on a suitable generalization of the random cluster model as a universal statistical tool. ...
The universality classes of equilibrium phase transitions of many statistical models are well known. On the other hand, very little is understood about the phenomenon of non-equilibrium criticality, including its existence. Nonetheless, from numerical simulations, it appears that memory effects are fundamental driving forces behind dynamic criticality. They are capable of establishing long-range order irrespective of the structure of the equilibrium model. A theoretical understanding of the role of memory in complex systems is important to understanding critical phenomenon as a whole. ...
In classical economics, a potential offender is treated as a rational agent that seeks to maximize the expected utility when deciding whether to commit a crime. Therefore, if the perceived threat of legal punishment outweights the gains from the crime action, then the offender is deterred. However, in reality, there are complex behavioral traits governing the risk perception of each individual that deviate from rationality. These effects need to be captured in order to construct a general model of deterrence. ...
On a signed graph (or spin glass), often times there are interactions that cannot be satisfied regardless of how one assigns the spin states. This property is known as frustration. The study of frustration of a bipartite graph is an active topic in graph theory, and has some important applications in unsupervised learning. For instance, a highly frustrated RBM has several desirable statistical properties, such as the correspondence between the joint and marginal distribution, that can be leveraged to achieve more efficient training. ...