Unlike ferromagnetic spin models, a spin glass has a highly non-trivial phase transition profile. For mean field models (the SK spin glass), the glass experiences a replica-symmetry breaking phenomenon that is only fully understood recently. However, for short-range models, almost nothing is known rigorously, including basic problems such as the nature of the glass transition. A potential route towards settling such problems may rely on a suitable generalization of the random cluster model as a universal statistical tool.
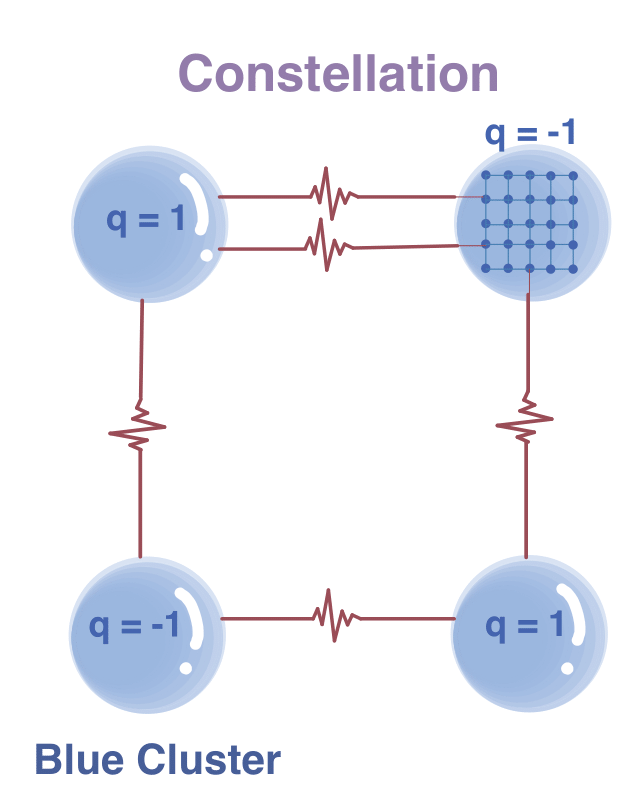
Using a graphical representation for the Ising spin-glass known as the Chayes-Machta-Redner (CMR) representation combined with a contour argument, we were able to rigorously prove the existence of a finite-temperature phsae transition for the Ising spin-glass of geometric nature. The low-temperature phase is characterized by the coexistence of multiple infinite clusters that are separated spatially and negatively correlated with each other in their spin-overlaps, as shown in the figure below.