The universality classes of equilibrium phase transitions of many statistical models are well known. On the other hand, very little is understood about the phenomenon of non-equilibrium criticality, including its existence. Nonetheless, from numerical simulations, it appears that memory effects are fundamental driving forces behind dynamic criticality. They are capable of establishing long-range order irrespective of the structure of the equilibrium model. A theoretical understanding of the role of memory in complex systems is important to understanding critical phenomenon as a whole.
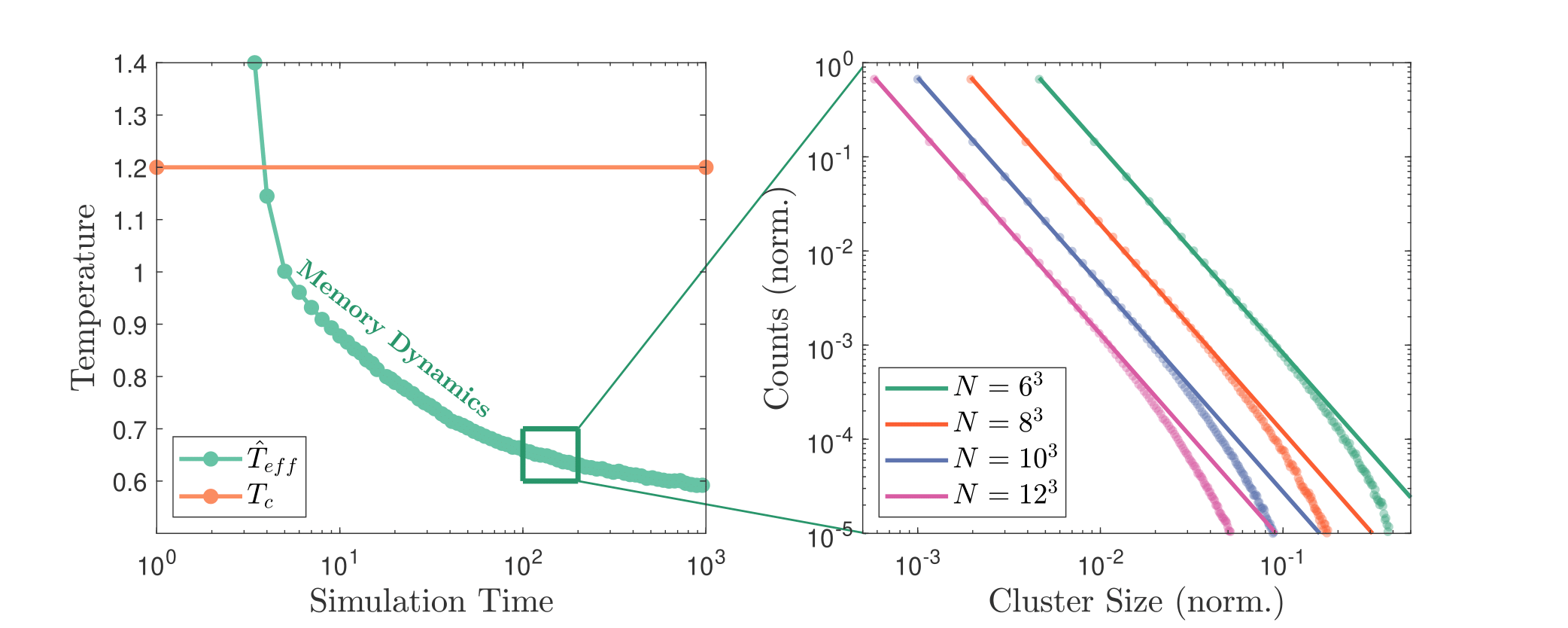
When we endow memory to a spin glass, the dynamics will act to steadily decrease the effective temperature of the glass (left figure), in a regime that is continuously near dynamic criticality (the polynomial cluster size distribution in the right figure).